Machine Learning Crash Course, Part I: Supervised Machine Learning

Artificial (Un)intelligence

When you type 'machine learning' into Google News, the first link you see is a Forbes Magazine piece called "What's The Difference Between Machine Learning And Artificial Intelligence?" This article contained so many flowery, grandiose descriptions about ML and AI technology that I couldn't help but laugh. A few notable quotes include:

1. "To get something out of machine learning, you need to know how to code or know someone who does. With artificial intelligence, you get something that takes an idea or a desire and runs with it, curiously seeking out new input and understandings."
2. "AI models don’t need to be rebuilt: they rebuild themselves. They actively seek out new and better sources of data."
3. "Your data is your cake mix, and your model is your method."

Addressing each quote in order:

1. AI algorithms (e.g. self-driving cars, video game playing robots) definitely do require coding. The 'running with desire' bit sounds like artificial general intelligence...which definitely doesn't exist.
2. If only this were true, I would never have to work again! One could maybe argue that reinforcement learning algorithms "rebuild" themselves, but a more accurate description would be that they're "recalibrating".
3. ... if you say so?

With all the nonsense the media uses to describe machine learning (ML) and artificial intelligence (AI), it's time we do a deep dive into what these technologies actually do. First, we need to learn the difference between AI and ML. Fortunately, a fellow writer has already written an excellent explanation. With that out of the way, we can focus on the ML side of things.

By definition, machine learning is the ability for computers to perform tasks without having to be explicitly programed. When writing a "normal" computer program, the coder will manually write out what the program will do, for every possible scenario. An ML program has a different style to it. Typically, the program will combine historical data, complex mathematical models and sophisticated algorithms to deduce the "optimal" behavior.

For instance, if you were writing a program to play checkers, a regular program might say something like "if I can jump over an opponent's piece, then I will do so". Instead, a machine learning program might say something like, "examine the last 1000 games of checkers I've played and pick the move that maximizes the probability that I will win the game".

Most machine learning algorithms fall into one of three categories: supervised learning, unsupervised learning, and reinforcement learning. In this article, we'll cover just the first of the three. 

Supervised Machine Learning

Supervised learning algorithms try to find a formula that accurately predicts the output label from input variables. Let’s clarify what this means with some simple, concrete examples.

1. Advertising Example (Linear Regression)

Suppose you work for an advertising agency and you want to predict the increased revenue after spending $100 in TV ads. Here, the input variable is advertising cost (TV) and the output label is revenue (Sales). If you had access to historical data about past advertising campaigns you could use a supervised learning algorithm like linear regression to find the answer. The table below lists the dollars spent on TV ads and the resulting sales from 200 advertising campaigns. 

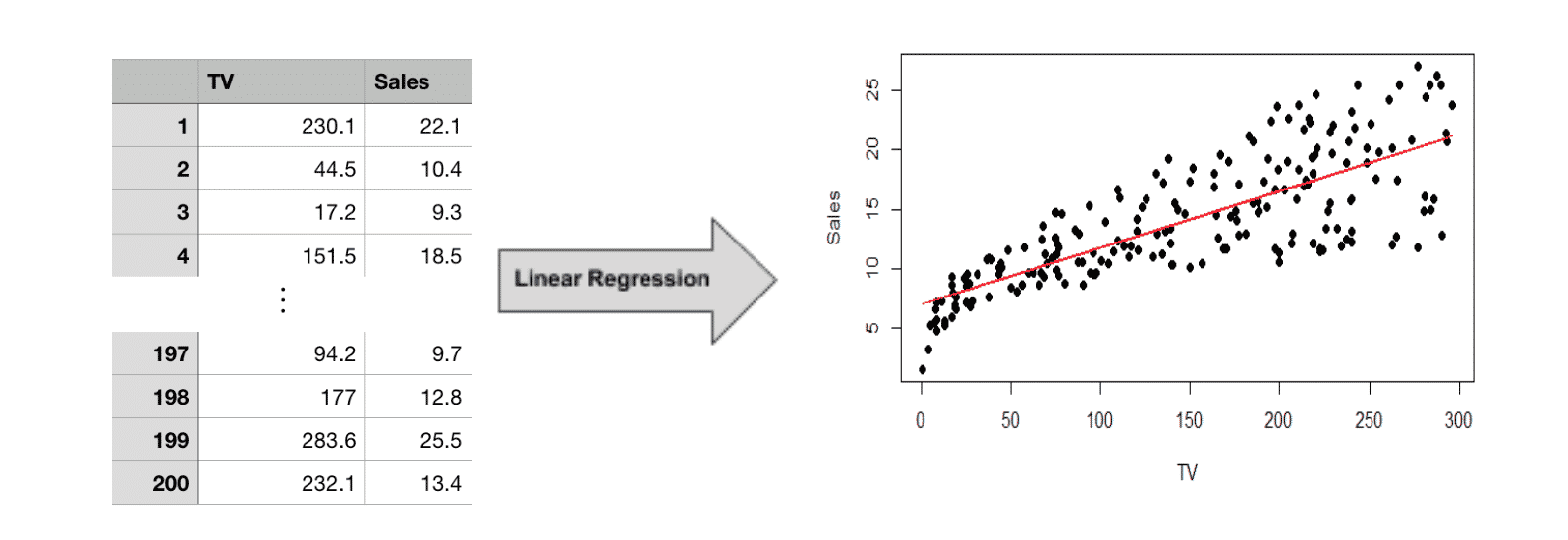
Image Credit: Leverege

First, we feed the historical data into our linear regression model. This produces a mathematical formula that predicts sales based on our input variable, TV ad spending:

Sales = 7.03 + 0.047(TV)

In the above graph, we have plotted both the historical data points (the black dots) as well as the formula our ML algorithm produces (the red line). The equation roughly follows the trajectory of the data points. To answer our original question of expected revenue, we can simply plug $100 in for the variable TV to get,

$11.73 = 7.03 + 0.047($100)

In other words, after spending 100 dollars on TV advertising, we can expect to generate only $11.73 in sales, based on past data. Therefore, it would probably be best to explore a different form of advertising. In summary, we used machine learning (specifically, linear regression) to predict how much revenue a TV advertising campaign would generate, based on historical data. 

2. Credit Card Example (Logistic Regression)

In the previous example, we mapped a numeric input (TV ad spending) to a numeric output (sales). However, it is also acceptable for the inputs/output to be categorical. When the output variable is categorical, then it is called a classification algorithm.

For example, a credit card company might want to predict whether a customer will default in the upcoming 3 months based on their current balance. Here, the output variable is categorical: it is either “yes” (the customer defaulted) or “no” (the customer did not default). As with the previous example, we need access to a dataset with labels that tell us whether or not the customer defaulted. We can then apply a classification algorithm like logistic regression.

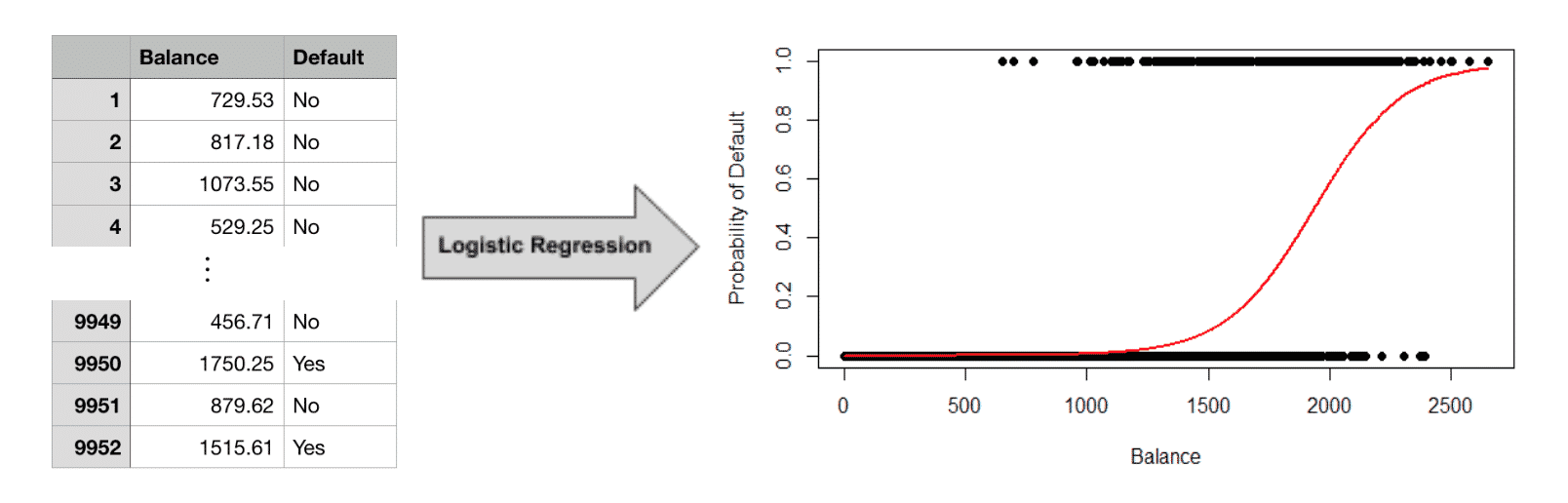
Image Credit: Leverege

The algorithm produces a more complex equation (red line) than linear regression. Previously, we were trying to predict an actual number (sales) so the output of our formula was a number ($11.73). However, we are no longer predicting a number. Instead we are predicting a category (“Yes, they will default within 3 months” or “No, they won’t default”).

The red line in the graph above represents the probability that someone will default based on their current balance. When a customer’s balance is less than 1000, the probability of default (red line) is near 0 (e.g. very unlikely to default). As a customer’s balance increases, so does the chances of default. We plotted the historical data in the graph as well, with “Yes” and “No” dummy coded as 1 and 0, respectively.

This equation can help you make predictions about new customers, where you aren’t told whether or not they will default in advance. From the logistic regression equation, you could check their balance, see that it’s only $400, and safely conclude they probably won’t default in three months. On the other hand, if their balance was $2500, you would know that they’re extremely likely to.

Conclusion

So far we've covered supervised machine learning, where we make predictions from labeled historical data. Stay tuned for the next part in the series where we cover unsupervised and reinforcement learning.